Gradient Correction beyond Gradient Descent
To improve the performance of a deep learning system, there are dozens of approaches one can take: enlarging the model structure by making it deeper or larger improving the initialization scheme collecting more data, or improving the optimization algorithm. This work aims to improve the model performance by advancing the quality of the gradient used by optimization algorithms
Among the most popular optimization algorithms, Gradient Descent (GD) has become the most common algorithm to optimize various kinds of neural networks. At the same time, most state-of-the-art artificial intelligence libraries contain implementations of various algorithms for optimizing gradient descent, there are three basic variants of GD: vanilla Batch gradient descent, stochastic gradient descent (SGD), and mini-batch gradient descent. Mini-batch gradient descent is a typical choice of the algorithm to train a neural network and the term SGD is also employed. However, vanilla SGD doesn’t guarantee good convergence. Therefore, more algorithms are proposed to deal with extant challenges of SGD, e.g., Momentum, Nesterov, Adagrad, Adadelta, RMSprop, Adam, Nadam, and so on. These methods mostly focus on modifying the gradients or the learning rate within the GD/SGD optimization framework.
Different from these methods, a gradient correction framework by introducing two plug-in modules: GC-W and GC-ODE to modify the calculated gradient. More specifically, the optimization path of GD is not always the optimal path to get to the objective.
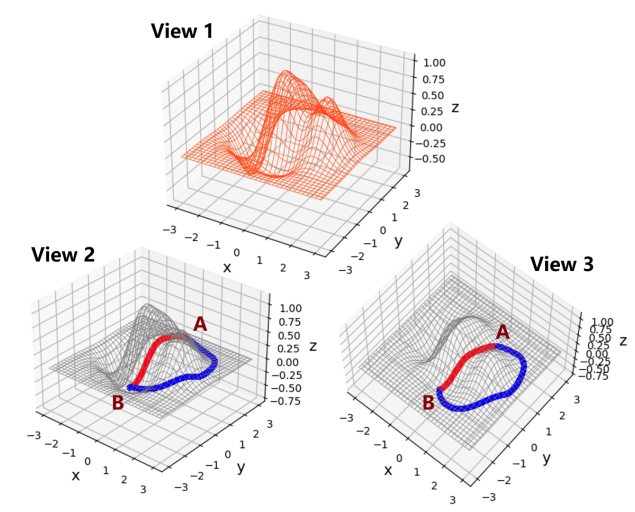
show a 2D surface from three different perspectives. Starting from
point A, we try to find the local minimal point B on this 2D
surface. The blue curve represents the optimization path found by
the vanilla gradient descent algorithm. The red curve represents
another path from A to B. Obviously, compared with the red one,
the blue path is not the optimal path to get to the destination. With
a proper modification on the gradient direction/scale, one can get
a better/faster path to the objective.
The layers before down-sampling are vital when performing gradient correction. This problem is handled from two aspects: 1) Weight gradient correction; 2) Hidden states gradient correction. Two plug-in modules are proposed respectively. Inspired by the idea of gradient prediction, the GC-W module for weight gradient correction, uses an attention-like structure to predict the gradient offset. The GC-W is optimized by the optimal gradient directions and scales according to the historical training information. For hidden states gradient correction, the neural ODE is used. The GCODE module is introduced to improve the gradient coherence of hidden states. As a plug-in branch, the GC-ODE module makes use of neural ODE layers to generate extra gradient data flow with dynamic system properties.
Gradient Correction for Weights
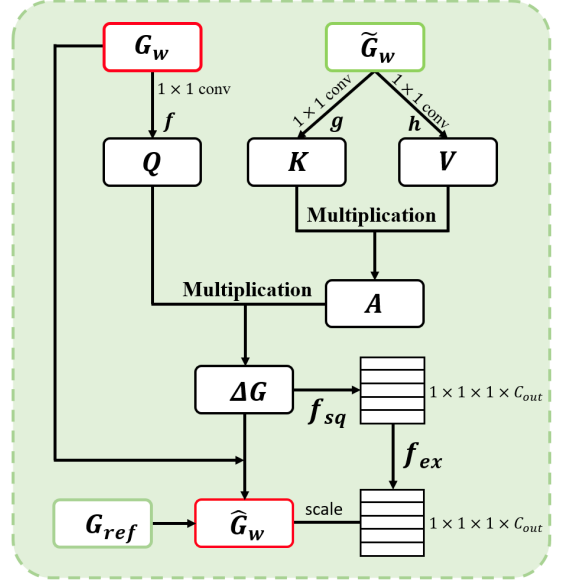
GC-W module performs gradient correction on the original weight
gradient Gw and outputs a new gradient Gˆw for back-propagation.
The GC-W module is trained asynchronously by the historical
training information (GW, Gew, Gref ).
The purpose of this GC-W (Gradient Correction for weights) module is to generate beneficial modifications for gradients. Suppose ∆G always corrects Gw to the ”right” direction, Gw can be replaced with Gˆw when updating the network weights during training. Optimization of the GC-W module follows an asynchronous policy.
Gradient Correction for the Hidden States
A neural network can be viewed as a dynamic system: φ(x(t), t), which is a function that describes the time dependence of a point x in a geometrical space. More specifically, let us take a neural network as an example. x(0) = x0 represents the initial state (i.e., the input tensor) of the network. x(1) = x1 represents the final state (i.e., the output tensor) of the network.
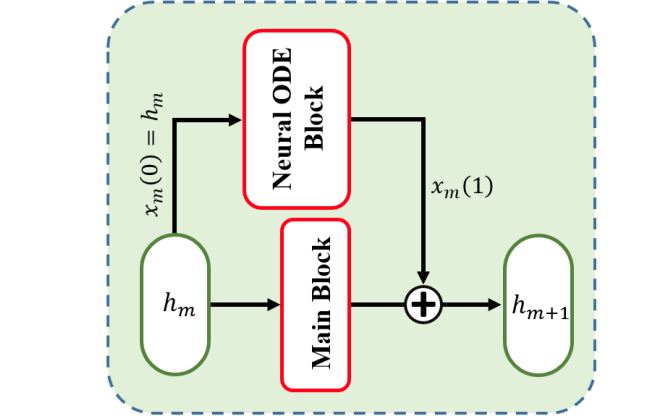
when we train a neural network, there is some incoherence or discontinuity in gradients of certain layers. To reveal the reason beneath, we associate the neural network with neural ODE. Similar to, We parameterize the derivative of the hidden state using a neural network.
dx(t)/dt = φ(x(t), t, θ)
Here, φ is a differentiable continuous function. θ is the parameter of φ. As claimed in, an ODE network defines a vector field, which continuously transforms the state. The derivative of the hidden state ∂x(t) ∂t is also continuous due to the property of φ(x(t), t, θ). Therefore, we propose to improve the between-layer gradient coherence of hidden states through a Neural ODE module.
Two gradient correction modules: GC-W and GC-ODE. We can combine these two modules (i.e., GC-W, GC-ODE) together as GCGD to do compound gradient correction. The overall framework is shown in Figure 5. We take ResNet-18 as an example. For all layers.
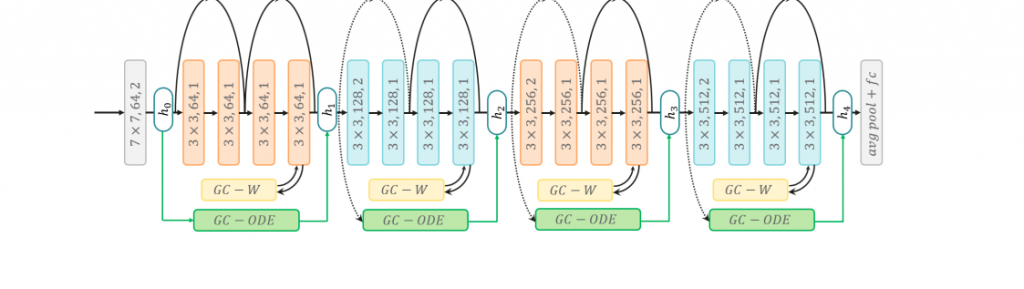
feature map resolution. The ResNet-20 for Cifar experiments has a similar structure with hidden states {h0, h1, h2, h3} and three pairs of
GC-W/GC-ODE modules.
before down-sampling, we insert the GC-W module. For hidden states {h0, h1, h2, h3, h4}, we insert GC-ODE module between adjacent pairs. Therefore, there are four pairs of GC-W and GC-ODE modules when applying GCGD to ResNet-18. Similarly, when applying GCGD to ResNet20 for Cifar-10, we use three pairs of GC-W and GC-ODE modules.

